IBM
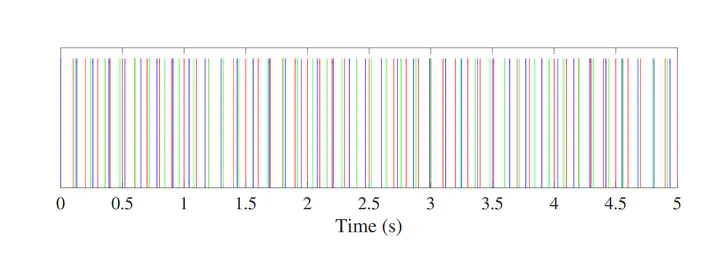 Digital controllers’ events
Digital controllers’ eventsSummary
Dynamic simulation of power systems provides the system’s response to a disturbance, which is a critical tool for optimally operating it. However, with increasing technological advancements and interconnecting neighbor networks, today’s power systems have become a very sparse network of heterogeneous devices. Some traditional devices such as synchronous machines have slower responses and some others such as electronic-based devices have faster responses. This leads to a system modeled with very stiff equations. Furthermore, the existence of different kinds of switches in the system such as breakers makes the system hybrid, i.e. the equations defining the system’s behavior may change at discrete points in time. Thus, Dynamic power system simulation requires solving numerous sets of nonlinear stiff hybrid Differential-Algebraic Equations (DAEs).
Digital controllers as components of any modern system introduce one event per each sampling. The figure above is an example of number of discontinuties forced to any system by three digital controllers with sampling rates equal to 0.1, 0.11, and 0.13 s. The most accurate method for treating any type of discontinuities in the time-domain simulation is the step-reduction method (SRM). In this way, the time step is reduced to land exactly on the event, the changes enforced by the discontinuity are applied, and the simulation restarts. However, SRM forces a heavy computation burden on the solver due to the constant step size reduction, which leads to increased simulation time for systems with many events.
The interpolation-based method (IBM) provides an accurate and computationally fast method to integrate the digital controllers in large time steps over multiple time events without reducing the time step. This is made possible by interpolating the state variables of the system at each digital controller sampling time and including the controller output in the DAEs model. In this way, the outputs of the controllers are estimated and corrected at each Newton iteration.